Answer:
8
Explanation:
Since we want to find the length of a line segment, we can use the distance formula.
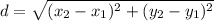
(x₁, y₁) and (x₂, y₂) are the points given.
The points we are given are: (-2,3) and (6,3). Therefore,
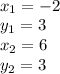
Plug each value into the formula.
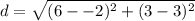
Evaluate inside of the parentheses first.
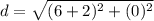
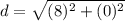
Evaluate the exponents.
8²= 8*8=64
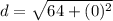
0²= 0*0= 0
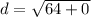
Add 64 and 0.

Take the square root of 64.
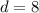
The length of the line segment is 8