By using the fact that,
When,

Then, With logarithm base a of a number b:

☃️So, Let's solve ths question....
To FinD:
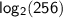
Let it be x,
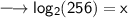
Proceeding further,

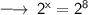
Then, We have same base 2, So
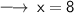
Or,
➙ log₂(256) = log₁₀(256) / log₁₀(2)
➙ log₂(256) = 2.40823996531 / 0.301029995664
➙ log₂(256) = 8
☕️ Hence, solved !!
━━━━━━━━━━━━━━━━━━━━