Answer:
the child is 1.581 m far from the fence
Step-by-step explanation:
The diagrammatic illustration that give a better view of what the question denote can be seen in the image attached below.
From the image attached below, let assume that the release point is the origin, then equation of the motion (x) is as follows:
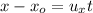
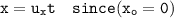 ---- (1)
---- (1)
the equation of the motion y is :
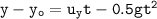
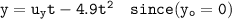
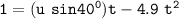
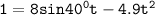
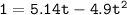
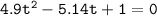
By using the quadratic formula, we have;
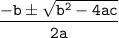
where;
a = 4.9, b = -5.14 c = 1
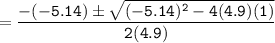
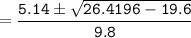
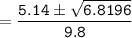
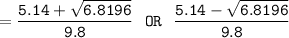
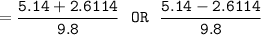
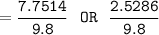
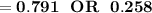
In as much as the ball is traveling upward, then we consider t= 0.258sec.
From equation (1)
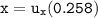
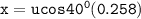
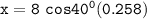
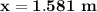
Thus, the child is 1.581 m far from the fence