Question

A rollercoaster is not moving and has 50,000 J of GPE at the top of a hill. How much kinetic energy will it have halfway down the hill, assuming there is no friction

Answer 1

The kinetic energy is 25000 J

Step-by-step explanation:

At the top of the hill, the potential energy = 50000 J

the potential energy = mgh

where m is the mass

g is the acceleration due to gravity

h is the vertical height at the top of the hill

Note the mass of the roller coaster and acceleration due to gravity will always remain constant, so that halfway down the hill, only the height changes by half its initial value.

This means that at halfway down the hill, the potential energy of the roller coaster is

PE =
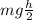`mg(h)/(2)` = 50000/2 = 25,000 J

We also know that the total mechanical energy of a system is given as

ME = KE + PE = constant

where

ME is the mechanical energy of the system

PE is the potential energy of the system

KE is the kinetic energy of the system

Let us now analyse.

At the top of the hill, all the mechanical energy of the roller coaster is equal to its potential energy due to the height on the hill above ground, since the roller coaster is not moving (kinetic energy is energy due to motion). Halfway down, the mechanical energy of the roller coaster is due to both the kinetic energy and the potential energy, since the roller coaster is moving down, and is still at a given height above the ground. Having all these in mind, we can proceed and say that at halfway down the hill, ignoring friction,

ME = KE + PE = constant

50000 = KE + 25000

therefore

KE = 25000 J