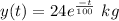Answer:
Explanation:
Let y(t) be the amount of salt in the tank after time t.
(A) Incoming rate = 0 (due to Pure water having no salt)
(B) Mixed solution comes out at 150 L/min. Initially the tank has 15,000 L of brine with 24 kg of salt.
concentration of salt at time t = y(t) / 15000 kg/L
Outgoing rate = y(t)/15000 * 150 = y(t) / 100
(C) we know that,
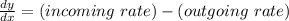
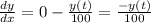
Separate variable and integrate
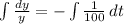
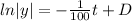
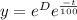
![y= Ce^{(-t)/(100) }\ [C=e^(D) ]](https://img.qammunity.org/2021/formulas/mathematics/high-school/8e6vufsur9zhkslidkztwr7jp386xelmwe.png)
At t= 0 , y(0) = 24 kg
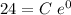
C= 24
(D) Therefore, the amount of salt in the tank after time t :