Answer and Step-by-step explanation:
Suppose that we have a number y which is a positive integer and that:
y =

Where;
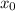 = digit at 10⁰ => one's place (units place)
= digit at 10⁰ => one's place (units place)
 = digit at 10¹ => 10's place (tens place)
= digit at 10¹ => 10's place (tens place)
 = digit at 10² => 100's place (hundreds place)
= digit at 10² => 100's place (hundreds place)
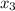 = digit at 10³ => 1000's place (thousands place)
= digit at 10³ => 1000's place (thousands place)
.
.
.
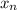 = digit at 10ⁿ place
= digit at 10ⁿ place
Then;
y =
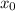 * 10⁰ +
* 10⁰ +
 * 10¹ +
* 10¹ +
 * 10² +
* 10² +
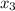 * 10³ +
* 10³ +
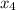 * 10⁴ +
* 10⁴ +
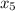 * 10⁵ + . . . +
* 10⁵ + . . . +
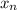 * 10ⁿ
* 10ⁿ
Since 10⁰ = 1, let's rewrite y as follows;
y =
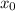 +
+
 * 10¹ +
* 10¹ +
 * 10² +
* 10² +
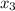 * 10³ +
* 10³ +
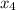 * 10⁴ +
* 10⁴ +
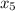 * 10⁵ + . . . +
* 10⁵ + . . . +
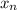 * 10ⁿ
* 10ⁿ
Now, to test if y is divisible by 11, replace 10 in the equation above by -1. Since 10 divided by 11 gives -1 (mod 11) [mod means modulus]
y =
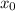 +
+
 * (-1)¹ +
* (-1)¹ +
 * (-1)² +
* (-1)² +
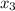 * (-1)³ +
* (-1)³ +
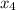 * (-1)⁴ +
* (-1)⁴ +
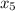 * (-1)⁵ + . . . +
* (-1)⁵ + . . . +
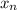 * (-1)ⁿ
* (-1)ⁿ
=> y =
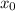 -
-
 +
+
 -
-
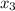 +
+
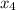 -
-
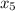 + . . . +
+ . . . +
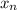 (-1)ⁿ (mod 11)
(-1)ⁿ (mod 11)
Therefore, it can be seen that, y is divisible by 11 if and only if alternating sum of its digits
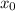 -
-
 +
+
 -
-
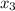 +
+
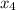 -
-
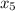 + . . . +
+ . . . +
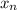 (-1)ⁿ is divisible by 11
(-1)ⁿ is divisible by 11
Let's take an example
Check if the following is divisible by 11.
i. 1859
Solution
1859 is divisible by 11 if and only if the alternating sum of its digit is divisible by 11. i.e if (1 - 8 + 5 - 9) is divisible by 11.
1 - 8 + 5 - 9 = -11.
Since -11 is divisible by 11 so is 1859
ii. 31415
Solution
31415 is divisible by 11 if and only if the alternating sum of its digit is divisible by 11. i.e if (3 - 1 + 4 - 1 + 5) is divisible by 11.
3 - 1 + 4 - 1 + 5 = 10.
Since 10 is not divisible by 11 so is 31415 not divisible.