Question

How many grams of PtBr4 will dissolve in 250.0 mL of water that has 1.00 grams of KBr dissolved in it

Answer 1

`m_(PtBr_4)=0.306gPtBr_4`

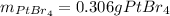
Step-by-step explanation:

Hello,

In this case, since the solubility product of platinum (IV) bromide is 8.21x10⁻⁹, and the dissociation is:

`PtBr_4(s)\rightleftharpoons Pt^(4+)(aq)+4Br^-(aq)`

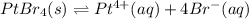
The equilibrium expression is:

`Ksp=[Pt^(4+)][Br^-]^4`

Thus, since the salt is added to a solution initially containing 1.00 grams of potassium bromide, there is an initial concentration of bromide ions:

`[Br^-]_0=(1.00gKBr*(1molKBr)/(119gKBr)*(1molBr^-)/(1molKBr) )/(0.250L)=0.0336M`

Hence, in terms of the molar solubility
`x`, we can write:

`8.21x10^(-9)=(x)(0.0336+4x)^4`

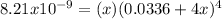
In such a way, solving for
`x`, we obtain:

`x=0.00238M`

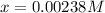
Which is the molar solubility of platinum (IV) bromide. Then, since its molar mass is 514.7 g/mol, we can compute the grams that get dissolved in the 250.0-mL solution:

`m_(PtBr_4)=0.00238(molPtBr_4)/(1L)*0.250L *(514.7gPtBr_4)/(1molPtBr_4) \\\\m_(PtBr_4)=0.306gPtBr_4`

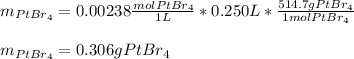
Best regards.