Question

If a diode at 300°K with a constant bias current of 100μA has a forward voltage of 700mV across it, what will the voltage drop across this same diode be if the bias current is increased to 1mA? g

Answer 1

the voltage drop across this same diode will be 760 mV

Step-by-step explanation:

Given that:

Temperature T = 300°K

current
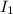`I_1` = 100 μA

current
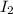`I_2` = 1 mA

forward voltage
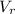`V_r` = 700 mV = 0.7 V

To objective is to find the voltage drop across this same diode if the bias current is increased to 1mA.

Using the formula:

`I = I_o \begin {pmatrix} e^{(V_r)/(nv_T)-1} \end {pmatrix}`

`I_1 = I_o \begin {pmatrix} e^{(V_r)/(nv_T)-1} \end {pmatrix}`

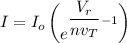
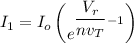
where;

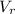`V_r` = 0.7

`I_1 = I_o \begin {pmatrix} e^{(0.7)/(nv_T)-1} \end {pmatrix}`

`I_2 = I_o \begin {pmatrix} e^{(V_r')/(nv_T)-1} \end {pmatrix}`

`(I_1)/(I_2) = \frac{ I_o \begin {pmatrix} e^{(0.7)/(nv_T)-1} \end {pmatrix} }{ I_o \begin {pmatrix} e^{(V_r')/(nv_T)-1} \end {pmatrix} }`

`(100 \ \mu A)/(1 \ mA) = \frac{ \begin {pmatrix} e^{(0.7)/(nv_T)-1} \end {pmatrix} }{ \begin {pmatrix} e^{(V_r')/(nv_T)-1} \end {pmatrix} }`

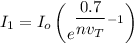
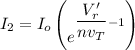
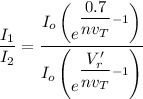
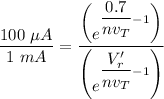
Suppose n = 1

`V_T = (T)/(11600) \\ \\ V_T = (300)/(11600) \\ \\ V_T = 25. 86 \ mV`

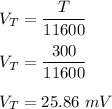
Then;

`e^{(V_r')/(nv_T)-1} = 10 \begin {pmatrix} e ^{\frac{ 0.7} { nV_T} -1} \end {pmatrix}`

`e^{(V_r')/(nv_T)-1} = 10 \begin {pmatrix} e ^{\frac{ 0.7} { 25.86} -1} \end {pmatrix}`

`e^{(V_r')/(nv_T)-1} = 5.699 * 10^(12)`

`{e^(V_r')/(nv_T)} = 5.7 * 10^(12)`

`{(V_r')/(nv_T)} =log_{e ^{5.7 * 10^(12)}}`

`{(V_r')/(nv_T)} =29.37`

`V_r'=29.37 * nV_T`

`V_r'=29.37 * 25.86`

`V_r'=759.5 \ mV`

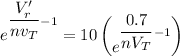
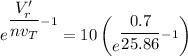
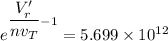
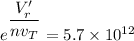
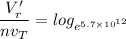
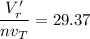
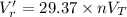
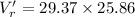
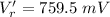
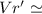`Vr' \simeq` 760 mV

Thus, the voltage drop across this same diode will be 760 mV