Question

A machine that produces ball bearings has initially been set so that the true average diameter of the bearings it produces is 0.500 in. A bearing is acceptable if its diameter is within 0.004 in. of this target value. Suppose, however, that the setting has changed during the course of production, so that the bearings have normally distributed diameters with a mean 0.499 in. and standard deviation 0.002 in. What percentage of bearings will now not be acceptable

Answer 1

the percentage of bearings that will not be acceptable = 7.3%

Explanation:

Given that:

Mean = 0.499

standard deviation = 0.002

if the true average diameter of the bearings it produces is 0.500 in and bearing is acceptable if its diameter is within 0.004 in.

Then the ball bearing acceptable range = (0.500 - 0.004, 0.500 + 0.004 )

= ( 0.496 , 0.504)

If x represents the diameter of the bearing , then the probability for the z value for the random variable x with a mean and standard deviation can be computed as follows:

`P(0.496\leq X \leq 0.504) = ((0.496 - \mu)/(\sigma) \leq (X -\mu)/(\sigma) \leq (0.504 - \mu)/(\sigma))`

`P(0.496\leq X \leq 0.504) = ((0.496 - 0.499)/(0.002) \leq (X -0.499)/(0.002) \leq (0.504 - 0.499)/(0.002))`

`P(0.496\leq X \leq 0.504) = ((-0.003)/(0.002) \leq Z \leq (0.005)/(0.002))`

`P(0.496\leq X \leq 0.504) = (-1.5 \leq Z \leq 2.5)`

`P(0.496\leq X \leq 0.504) = P (-1.5 \leq Z \leq 2.5)`

`P(0.496\leq X \leq 0.504) = P(Z \leq 2.5) - P(Z \leq -1.5)`

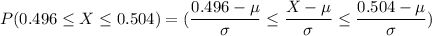
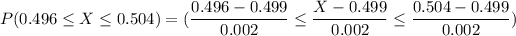
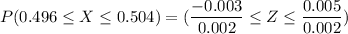
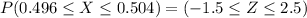
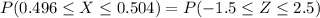
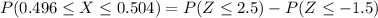
From the standard normal tables

`P(0.496\leq X \leq 0.504) = 0.9938-0.0668`

`P(0.496\leq X \leq 0.504) = 0.927`

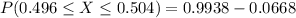
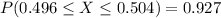
By applying the concept of probability of a complement , the percentage of bearings will now not be acceptable

P(not be acceptable) = 1 - P(acceptable)

P(not be acceptable) = 1 - 0.927

P(not be acceptable) = 0.073

Thus, the percentage of bearings that will not be acceptable = 7.3%