Answer: μ = 0.8885
Explanation: Force due to friction is calculated as:

At an inclined plane, normal force (N) is: N = mgcosθ, in which θ=32.51.
Power associated with work done by friction is
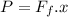 . The variable x is displacement the object "spent its energy".
. The variable x is displacement the object "spent its energy".
Power associated with work done by gravitational force is P = mghcosθ, where h is height.
The decline forms with horizontal plane a triangle as draw in the picture.
To determine force due to friction:
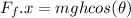
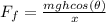
Replacing force:
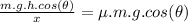
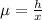
Calculating h using trigonometric relations:
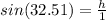
h = sin(32.51)
Coefficient of Kinetic friction is
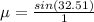
μ = 0.8885
For these conditions, coefficient of kinetic friction is μ = 0.8885.