Question

Chromium-51 is a radioisotope that is used to assess the lifetime of red blood cells The half-life of chromium-51 is 27.7 days. If you begin with 48.0 mg of this isotope, what mass remains after 47.9 days have passed?

Answer 1

After 47.9 days, will remain 14.5mg of the isotope

Step-by-step explanation:

The radioactive decay follows always first-order kinetics where its general law is:

Ln[A] = -Kt + ln[A]₀

Where [A] is actual concentration of the atom, k is rate constant, t is time and [A]₀ is initial concentration.

We can find rate constant from half-life as follows:

`t_(1/2) = (ln2)/(K)`

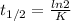
K = ln 2 / 27.7 days

K = 0.025 days⁻¹

Replacing, initial amount of isotope is 48.0mg = [A]₀ , K is 0.025 days⁻¹ and t = 47.9 days:

Ln[A] = -Kt + ln[A]₀

Ln[A] = -0.025 days⁻¹*47.9 days + ln (48.0mg)

ln [A] = 2.6726

[A] = e^ (2.6726)

[A] = 14.5mg

After 47.9 days, will remain 14.5mg of the isotope