Question

How many petals are on the graph? Find the trigonometric form of a given function.

Answer 1

Attachment 1 : Option A,

Attachment 2 : Option C

Explanation:

( 1 ) Here we know that " n " is 6. Now remember if n is odd, the number of petals on the graph will be n. However if n is even, the number of petals on the graph will be 2n.

6 is even, and hence the number of petals will be 2(6) = 12 petals. Solution : 12 petals

( 2 ) To solve such problems we tend to use the equation
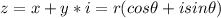`z = x + y * i = r(cos\theta +isin\theta)` where
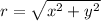`r = √(x^2+y^2)` etc. Here I find it simpler to see each option, and convert each into it's standard complex form. It might seem hard, but it is easy if you know the value of (cos(5π / 3)) etc...

The answer here will be option c, but let's prove it,

cos(5π / 3) = 1 / 2,

sin(5π / 3) =
`-(√(3))/(2)`

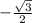
Plugging those values in for "
`8\left(\cos \left((5\pi )/(3)\right)+i\sin \left((5\pi )/(3)\right)\right)` "

`8\left(-(√(3)i)/(2)+(1)/(2)\right)`

=
`8\cdot (1)/(2)-8\cdot (√(3)i)/(2)` =
`4-4√(3)i`

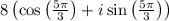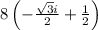
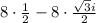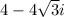
Hence proved that your solution is option c.