Question

Given that a random variable X is normally distributed with a mean of 2 and a variance of 4, find the value of x such that P(X < x)

Answer 1

Given that a random variable X is normally distributed with a mean of 2 and a variance of 4, find the value of x such that P(X < x)=0.99 using the cumulative standard normal distribution table

Answer:

6.642

Explanation:

Given that mean = 2

standard deviation = 2

Let X be the random Variable

Then X
`\sim` N(n,
`\sigma`)

X
`\sim` N(2,2)

By Central limit theorem;

`z = (X - \mu)/(\sigma) \sim N(0,1)`

`z = (X - 2)/(2) \sim N(0,1)`

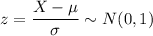
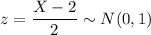
P(X<x) = 0.09

`P(Z < (X-\mu)/(\sigma ))= 0.99`

`P(Z < (X-2)/(2))= 0.99`

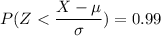
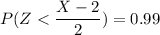
P(X < x) = 0.99

`P((X-2)/(2)< (X-2)/(2))=0.99`

`P(Z< (X-2)/(2))=0.99`

`\phi ( (X-2)/(2))=0.99`

`( (X-2)/(2))= \phi^(-1) (0.99)`

`( (X-2)/(2))= 2.321`

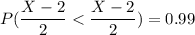
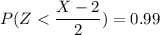
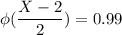
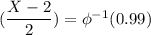
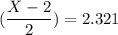
X -2 = 2.321 × 2

X -2 = 4.642

X = 4.642 +2

X = 6.642