Answer:
Explanation:
Hello, when you try to find the intersection point(s) you need to solve a system like this one
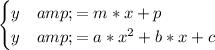
So, you come up with a polynomial equation like.
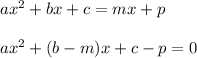
And then, we can estimate the discriminant.

If
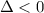 there is no real solution, no intersection point.
there is no real solution, no intersection point.
If
 there is one intersection point.
there is one intersection point.
If
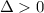 there are two real solutions, so two intersection points.
there are two real solutions, so two intersection points.
Hope this helps.