Question

5. During a national debate on changes to health care, a cable news service performs an opinion poll of 500 small business owners. It shows that 65% of small-business owners do not approve of health care changes. Develop a 95% confidence interval for the proportion opposing health care changes. Use 4 decimal places.

Answer 1

The 95% confidence interval for the proportion opposing health care changes is (0.6082, 0.6918).

Explanation:

The (1 - α)% confidence interval for the population proportion is:

`CI=\hat p\pm z_(\alpha/2)\cdot\sqrt{(\hat p(1-\hat p))/(n)}`

The information provided is:

`\hat p=0.65\\n=500\\\text{Confidence level}=95\%`

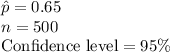
The critical value of z for 95% confidence level is:

`z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

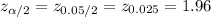
*Use a z-table.

Compute the 95% confidence interval for the proportion opposing health care changes as follows:

`CI=\hat p\pm z_(\alpha/2)\cdot\sqrt{(\hat p(1-\hat p))/(n)}`

`=0.65\pm 1.96\sqrt{(0.65(1-0.65))/(500)}\\\\=0.65\pm 0.04181\\\\=(0.60819, 0.69181)\\\\\approx (0.6082, 0.6918)`

Thus, the 95% confidence interval for the proportion opposing health care changes is (0.6082, 0.6918).