Answer:
The 95% confidence interval for the proportion opposing health care changes is (0.6082, 0.6918).
Explanation:
The (1 - α)% confidence interval for the population proportion is:
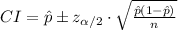
The information provided is:
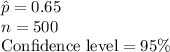
The critical value of z for 95% confidence level is:
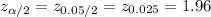
*Use a z-table.
Compute the 95% confidence interval for the proportion opposing health care changes as follows:
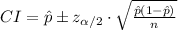

Thus, the 95% confidence interval for the proportion opposing health care changes is (0.6082, 0.6918).