Question

Beginning 177 miles directly north of the city of Morristown, a van travels due west. If the van is travelling at a speed of 31 miles per hour, determine the rate of change of the distance between Morristown and the van when the van has been travelling for 71 miles. (Do not include units in your answer, and round to the nearest hundredth.)

Answer 1

Explanation:

From the given information;

let the hypotenuse be a , the opposite which is the north direction be b and the west direction which is the adjacent be c

SO, using the Pythagoras theorem

a² = c² + 177²

By taking the differentiation of both sides with respect to time t , we have

`2a (da)/(dt) = 2c (dc)/(dt) + 0`

`(da)/(dt) = (c)/(a) (dc)/(dt)`

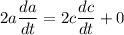
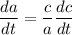
At c = 71 miles,
`a = √( (71)^2 +(177)^2)`

`a = √( 5041+31329)`

`a = √( 36370)`

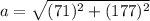
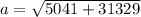
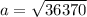
a = 190.71

SImilarly,
`(dc)/(dt) = \ 31 miles \ / hr`

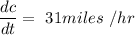
Thus, the rate of change of the distance between Morristown and the van when the van has been travelling for 71 miles can be calculate as:

`(da)/(dt) = (c)/(a) (dc)/(dt)`

`(da)/(dt) = (71)/(190.71) * 31`

`(da)/(dt) = 0.37229 * 31`

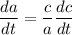
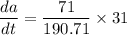
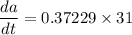
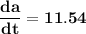`\mathbf{(da)/(dt) = 11.54}` to the nearest hundredth.