Question

F

19) The points (6,5), (7,2), (9,6), and (10,3) are vertices of an inscribed square.
A)(x - 8)2-(y - 4)2 = 5
B) (x – 8)2 + (y - 4)2 = 15
C) (X + 8)2 + (y + 4)2 = 5
D) (x - 8)2 + (y - 4)2 = 5
Find an equation for the circle

Answer 1

The equation of circle is
`(x-8)^2+(y-4)^2=5`

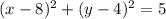
(D) is correct option.

Explanation:

Given that,

Points (6,5), (7,2), (9,6) and (10,3) are vertices of an inscribed square.

We need to calculate the distance between (7,2) and (9,6)

Using formula of distance

`d=\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`

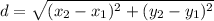
Put the value into the formula

`d^2=(9-7)^2+(6-2)^2`

`d^2=20\ m`

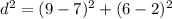
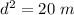
The radius will be

`r^2=(20)/(4)`

`r^2=5`

We need to calculate the center of the point (7,2) and (9,6)

Using formula of center point

For x axis,

`h=(x_(2)+x_(1))/(2)`

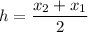
Put the value into the formula

`h=(9+7)/(2)`

`h=(16)/(2)`

`h=8`

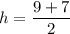
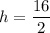
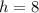
For y axis,

`k=(y_(2)+y_(1))/(2)`

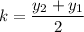
Put the value into the formula

`k=(6+2)/(2)`

`k=(8)/(2)`

`k=4`

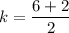
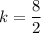
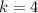
We need to find the equation for the circle

Using formula of equation of circle

`(x-h)^2+(y-k)^2=r^2`

Put the value into the formula

`(x-8)^2+(y-4)^2=5`

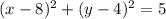
Hence, The equation of circle is
`(x-8)^2+(y-4)^2=5`

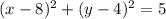
(D) is correct option.