Question

Determine the orbital period (in hours) of an observation satellite in a circular orbit 1,787 km above Mars.

Answer 1

T = 3.14 hours

Step-by-step explanation:

We need to find the orbital period (in hours) of an observation satellite in a circular orbit 1,787 km above Mars.

We know that the radius of Mars is 3,389.5 km.

So, r = 1,787 + 3,389.5 = 5176.5 km

Using Kepler's law,

`T^2=(4\pi ^2)/(GM)r^3`

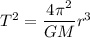
M is mass of Mars,
`M=6.39* 10^(23)\ kg`

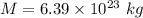
So,

`T^2=(4\pi ^2)/(6.67* 10^(-11)* 6.39* 10^(23))* (5176.5 * 10^3)^3\\\\T=\sqrt{(4\pi^(2))/(6.67*10^(-11)*6.39*10^(23))*(5176.5*10^(3))^(3)}\\\\T=11334.98\ s`

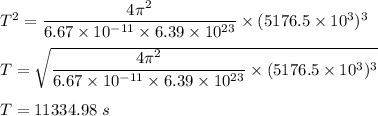
or

T = 3.14 hours

So, the orbital period is 3.14 hours