Question

In how many ways can a subcommittee of 6 students be chosen from a committee which consists of 10 senior members and 12 junior members if the team must consist of 4 senior members and 2 junior members?

Answer 1

The number of ways is 13860 ways

Explanation:

Given

Senior Members = 10

Junior Members = 12

Required

Number of ways of selecting 6 students students

The question lay emphasis on the keyword selection; this implies combination

From the question, we understand that

4 students are to be selected from senior members while 2 from junior members;

The number of ways is calculated as thus;

Ways = Ways of Selecting Senior Members * Ways of Selecting Junior Members

`Ways = ^(10)C_4 * ^(12)C2`

`Ways = (10!)/((10-4)!4!)) * (12!)/((12-2)!2!))`

`Ways = (10!)/((6)!4!)) * (12!)/((10)!2!))`

`Ways = (10 * 9 * 8 * 7 *6!)/((6! * 4*3*2*1)) * (12*11*10!)/((10!*2*1))`

`Ways = (10 * 9 * 8 * 7)/(4*3*2*1) * (12*11)/(2*1)`

`Ways = (5040)/(24) * (132)/(2)`

`Ways = 210 * 66`

`Ways = 13860`

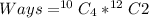
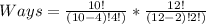
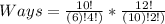
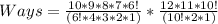
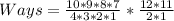
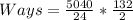
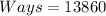
Hence, the number of ways is 13860 ways