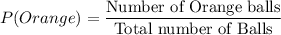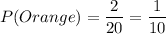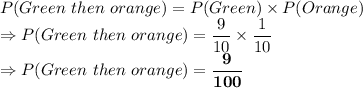Answer:
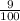
Explanation:
Given:
Number of red balls, n(R) = 3
Number of green balls, n(G) = 9
Number of yellow balls, n(Y) = 2
Number of orange balls, n(O) = 2
Number of purple balls, n(P) = 4
Two balls are drawn one at a time with replacement.
To find:
Probability of drawing a green ball and an orange ball ?
Solution:
Total number of balls, n(Total) = 3 + 9 + 2 + 2 + 4 = 20
Formula for probability of an event E is given as:
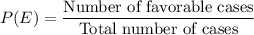
Probability that a green ball is drawn at first:
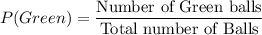

Now, the ball is replaced , so total number of balls remain the same i.e. 20.