Question

g A chemist combines 59.9 mL of 0.282 M potassium bromide with 15.4 mL of 0.512 M silver nitrate. (a) How many grams of silver bromide will precipitate

Answer 1

`m_(AgBr)=1.48gAgBr`

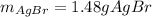
Step-by-step explanation:

Hello,

In this case, the undergoing chemical reaction is:

`KBr(aq)+AgNO_3(aq)\rightarrow AgBr(s)+KNO_3(aq)`

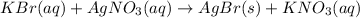
Thus, since the potassium bromide and silver nitrate are in a 1:1 mole ratio, the first step is to identify the limiting reactant, by considering the reacting volumes of reactants in order to compute the available moles of potassium bromide and the moles of potassium bromide consumed by the 15.4 mL of 0.512-M solution of silver nitrate:

`n_(KBr)=0.0599L*0.282(molKBr)/(L) =0.0169molKBr\\\\n_(KBr)^(consumed)=0.0154L*0.512(molAgNO_3)/(L) *(1molKBr)/(1molAgNO_3)=0.00788molKBr`

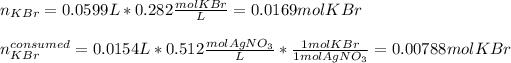
In such a way, since less moles are consumed than available, we infer that silver nitrate is the limiting reactant, for which the resulting grams of silver bromide (molar mass 187.8 g/mol) result:

`m_(AgBr)=0.00788molAgNO_3*(1molAgBr)/(1molAgNO_3) *(187.8gAgBr)/(1molAgBr) \\\\m_(AgBr)=1.48gAgBr`

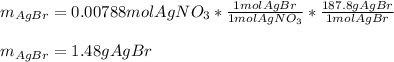
Best regards.