Answer:
Attachment 1 : Option C
Attachment 2 : Option A
Explanation:
( 1 ) Expressing the product of z1 and z2 would be as follows,
![14\left[\cos \left((\pi \:)/(5)\right)+i\sin \left((\pi \:\:)/(5)\right)\right]\cdot \:2√(2)\left[\cos \left((3\pi \:)/(2)\right)+i\sin \left((3\pi \:\:)/(2)\right)\right]](https://img.qammunity.org/2021/formulas/mathematics/college/rj9jx84wzuquke5fmdhoeo66ckhhg02o1n.png)
Now to solve such problems, you will need to know what cos(π / 5) is, sin(π / 5) etc. If you don't know their exact value, I would recommend you use a calculator,
cos(π / 5) =
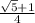 ,
,
sin(π / 5) =
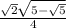
cos(3π / 2) = 0,
sin(3π / 2) = - 1
Let's substitute those values in our expression,
![14\left[(√(5)+1)/(4)+i\frac{√(2)\sqrt{5-√(5)}}{4}\right]\cdot \:2√(2)\left[0-i\right]](https://img.qammunity.org/2021/formulas/mathematics/college/kv22f9kmvgq2klhr1efs0qbqkf2aptw5pj.png)
And now simplify the expression,
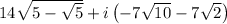
The exact value of
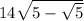 =
=
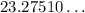 and
and
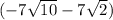 =
=
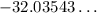 Therefore we have the expression
Therefore we have the expression
 , which is close to option c. As you can see they approximated the solution.
, which is close to option c. As you can see they approximated the solution.
( 2 ) Here we will apply the following trivial identities,
cos(π / 3) =
 ,
,
sin(π / 3) =
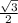 ,
,
cos(- π / 6) =
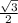 ,
,
sin(- π / 6) =
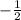
Substitute into the following expression, representing the quotient of the given values of z1 and z2,
![15\left[cos\left((\pi \:)/(3)\right)+isin\left((\pi \:\:)/(3)\right)\right] / \:3√(2)\left[cos\left((-\pi \:)/(6)\right)+isin\left((-\pi \:\:)/(6)\right)\right]](https://img.qammunity.org/2021/formulas/mathematics/college/h9ouclzg6bbjw0udkudj97wfa5q8h1k48q.png) ⇒
⇒
![15\left[(1)/(2)+(√(3))/(2)\right]/ \:3√(2)\left[(√(3))/(2)+-(1)/(2)\right]](https://img.qammunity.org/2021/formulas/mathematics/college/rccnglcfhp0rqq7qipf1f8jfhi793xyp9g.png)
The simplified expression will be the following,
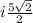 or in other words
or in other words
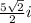 or
or
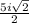
The solution will be option a, as you can see.