Answer:
248.26 cm²
Explanation:
Surface area of the composite figure = (surface area of cuboid + surface area of hemisphere) - 2(base area of hemisphere)
Surface area of cuboid =
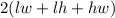
Where,
l = 10 cm
w = 5 cm
h = 4 cm
Plug in the values into the formula:
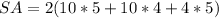
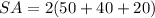
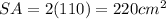
Surface area of hemisphere = 3πr²
Where,
π = 3.14
r = 3 cm
SA of hemisphere = 3*3.14*3² = 3*3.14*9 = 84.78 cm²
Base area of hemisphere = πr²
BA = 3.14*3² = 3.14*9 = 28.26 cm²
Surface area of the composite shape = (220 + 84.78) - 2(28.26)
= 304.78 - 56.52
SA = 248.26 cm²