Question

An object is made of glass and has the shape of a cube 0.13 m on a side, according to an observer at rest relative to it. However, an observer moving at high speed parallel to one of the object's edges and knowing that the object's mass is 2.0 kg determines its density to be 7300 kg/m3, which is much greater than the density of glass. What is the moving observer's speed (in units of c) relative to the cube

Answer 1

The velocity is
`v = 2.6*10^(8) \ m/s`

Step-by-step explanation:

From the question we are told that

The side of the cube is
`l = 0.13 \ m`

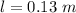
The mass of the object is
`m = 2.0 \ kg`

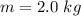
The density of the object is
`\rho = 7300 \ kg / m^3`

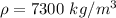
Generally the volume of the object according to the moving observer is mathematically represented as

`V =(m)/(\rho)`

`V =(2)/(7300)`

`V = 2.74*10^(-4) \ m^3`

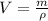
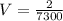
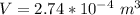
Therefore the length of the side as observed by the observer on high speed is mathematically represented as

`L = \sqrt[3]{V}`

`L = \sqrt[3]{2.74 *10^(-4)}`

`L =0.065`

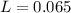
Now the original length of side is mathematically represented as

`L= l * \sqrt{ (1 - ( ( v)/(c))^2 )}`

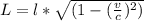
Where c is the speed of light with value
`c = 3.0*10^(8) \ m/s`

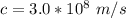
So

`v = \sqrt{1 - [(L)/(l)]^2} * c`

=>
`v = \sqrt{1 - [(0.065)/(0.13)]^2} * c`

=>
`v = 2.6*10^(8) \ m/s`