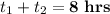Answer:
8 hours
Explanation:
Given:
Sheyna drives to the lake with average speed of 60 mph and
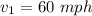
Sheyna drives back from the lake with average speed of 36 mph
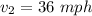
It took 2 hours less time to get there than it did to get back.
Let
 be the time taken to drive to lake.
be the time taken to drive to lake.
Let
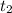 be the time taken to drive back from lake.
be the time taken to drive back from lake.
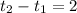 hrs ..... (1)
hrs ..... (1)
To find:
Total time taken = ?
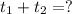
Solution:
Let D be the distance to lake.
Formula for time is given as:
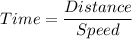
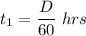
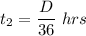
Putting in equation (1):
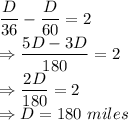
So,
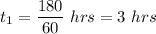
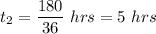
So, the answer is: