Complete Question
What is the minimum sample size required to estimate a population mean with 90% confidence when the desired margin of error is 1.25? The standard deviation in a pre-selected sample is 7.5
Answer:
The minimum sample size is

Explanation:
From the question we are told that
The margin of error is
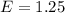
The standard deviation is
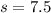
Given that the confidence level is 90% then the level of significance is mathematically represented as
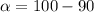
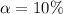

Next we obtain the critical value of
 from the normal distribution table
from the normal distribution table
The value is

The minimum sample size is mathematically evaluated as
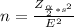
=>
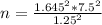
=>
