Question

The solutions to \[2x^2 - 10x + 13 = 0\]are $a+bi$ and $a-bi,$ where $a$ and $b$ are positive. What is $a\cdot b?$
`The solutions to\[2x^2 - 10x + 13 = 0\]are $a+bi$ and $a-bi,$ where $a$ and $b$ are positive. What is $a\cdot b?$`

Answer 1

Answer: 5/4

In decimal form, this is equivalent to 1.25

=============================================

Work Shown:

The given equation 2x^2-10x+13 = 0 matches the form ax^2+bx+c = 0

We see that a = 2, b = -10, c = 13. Plug those values into the quadratic formula to solve for x.

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-(-10)\pm√((-10)^2-4(2)(13)))/(2(2))\\\\x = (10\pm√(-4))/(4)\\\\x = (10\pm2i)/(4)\\\\x = (2(5\pm i))/(2*2)\\\\x = (5\pm i)/(2)\\\\x = (5)/(2) \pm (1)/(2)i\\\\x = (5)/(2) + (1)/(2)i \ \text{ or } \ x = (5)/(2) - (1)/(2)i\\\\`

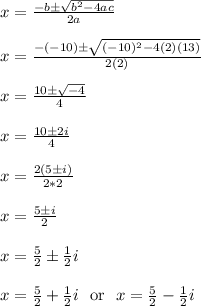
The two solutions are in the form
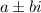`a \pm bi` where a = 5/2 and b = 1/2

Therefore a*b = (5/2)*(1/2) = 5/4 = 1.25