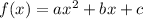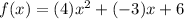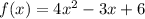Question

Given the following three points, find by the hand the quadratic function they represent (0,6, (2,16, (3,33)

Answer 1

`f(x) = 4x^2 - 3x + 6`

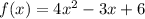
Explanation:

Quadratic function is given as
`f(x) = ax^2 + bx + c`

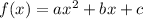
Let's find a, b and c:

Substituting (0, 6):

`6 = a(0)^2 + b(0) + c`

`6 = 0 + 0 + c`

`c = 6`

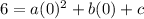
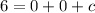
Now that we know the value of c, let's derive 2 system of equations we would use to solve for a and b simultaneously as follows.

Substituting (2, 16), and c = 6

`f(x) = ax^2 + bx + c`

`16 = a(2)^2 + b(2) + 6`

`16 = 4a + 2b + 6`

`16 - 6 = 4a + 2b + 6 - 6`

`10 = 4a + 2b`

`10 = 2(2a + b)`

`(10)/(2) = (2(2a + b))/(2)`

`5 = 2a + b`

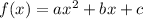
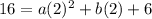
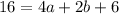
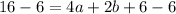
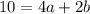
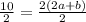
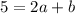
`2a + b = 5` => (Equation 1)

Substituting (3, 33), and c = 6

`f(x) = ax^2 + bx + x`

`33 = a(3)^2 + b(3) + 6`

`33 = 9a + 3b + 6`

`33 - 6 = 9a + 3b + 6 - 6`

`27 = 9a + 3b`

`27 = 3(3a + b)`

`(27)/(3) = (3(3a + b))/(3)`

`9 = 3a + b`

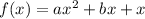
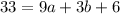
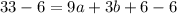
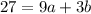
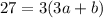
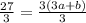
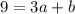
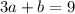`3a + b = 9` => (Equation 2)

Subtract equation 1 from equation 2 to solve simultaneously for a and b.

`3a + b = 9`

`2a + b = 5`

`a = 4`

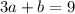
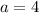
Replace a with 4 in equation 2.

`2a + b = 5`

`2(4) + b = 5`

`8 + b = 5`

`8 + b - 8 = 5 - 8`

`b = -3`

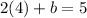
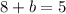
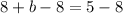
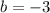
The quadratic function that represents the given 3 points would be as follows:

`f(x) = ax^2 + bx + c`

`f(x) = (4)x^2 + (-3)x + 6`

`f(x) = 4x^2 - 3x + 6`