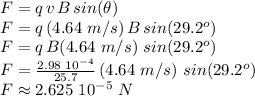Answer:
The magnetic force would be:
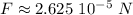
Step-by-step explanation:
Recall that the magnetic force on a charged particle (of charge q) moving with velocity (v) in a magnetic field B, is given by the vector product:
F = q v x B
(where the bold represents vectors)
the vector product involves the sine of the angle (
 ) between the vectors, so we can write the relationship between the magnitudes of these quantities as:
) between the vectors, so we can write the relationship between the magnitudes of these quantities as:

Therefore replacing the known quantities for the first case:
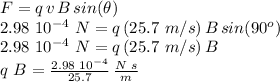
Now, for the second case, we can find the force by using this expression for the product of the particle's charge times the magnetic field, and the new velocity and angle: