Question

The values of the sample mean, sample standard deviation, and (estimated) standard error of the mean are 2.482, 1.614, and 0.295, respectively. Does this data suggest that the true average percentage of organic matter in such soil is something other than 3%

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

Yes the test suggest that the true average percentage of organic matter in such soil is something other than 3%

Explanation:

From the question we are told that

The sample mean is
`\= x = 2.482\%`

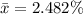
The standard deviation is
`\sigma = 1.614`

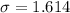
The standard error is
`SE = 0.295`

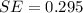
The sample size is
`n = 30`

The level of significance is
`\alpha = 0.05`

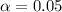
The null hypothesis is
`H_o : \mu = 3\%`

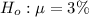
The alternative hypothesis is
`H_a : \mu \\e 3\%`

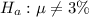
Now the degree of freedom is evaluated as

`df = n - 1`

`df = 30 - 1`

`df = 29`

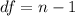
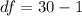
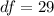
The test statistics is mathematically evaluated as

`t = ( 2.482 - 3)/( 0.295)`

`t = -1.756`

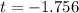
The p-value is obtained from the the student t -distribution table , the value is

`p-value = P( T \le t)= 2 * t_( t, df ) = t_( -1.756 , 29 ) = 2 *0.0448= 0.0896`

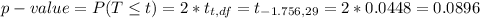
The reason for the 2 in the equation is because the test is a two -tailed test i.e -1.756 and 1.756

Given that the
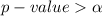`p-value > \alpha` then we fail to reject the null hypothesis

Hence the test the suggest that the true average percentage of organic matter in such soil is something other than 3%