Question

Find the maximum rate of change of f at the given point and the direction in which it occurs. f(x, y) = 8 sin(xy), (0, 9)

Answer 1

The maximum rate of change of f at (0, 9) is 72 and the direction of the vector is
`\mathbf{\hat i}`

Explanation:

Given that:

F(x,y) = 8 sin (xy) at (0,9)

The maximum rate of change f(x,y) occurs in the direction of gradient of f which can be estimated as follows;

`\overline V f (x,y) = \begin {bmatrix} (\partial )/(\partial x ) (x,y) \hat i \ + \ (\partial )/(\partial y ) (x,y) \hat j \end {bmatrix}`

`\overline V f (x,y) = \begin {bmatrix} (\partial )/(\partial x ) (8 \ sin (xy) \hat i \ + \ (\partial )/(\partial y ) (8 \ sin (xy) \hat j \end {bmatrix}`

`\overline V f (x,y) = \begin {bmatrix} (8y \ cos (xy) \hat i \ + \ (8x \ cos (xy) \hat j \end {bmatrix}`

`| \overline V f (0,9) |= \begin {vmatrix} 72 \hat i + 0 \end {vmatrix}`

`\mathbf`

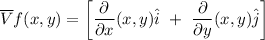
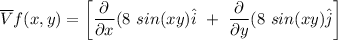
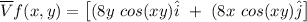
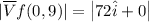
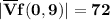
We can conclude that the maximum rate of change of f at (0, 9) is 72 and the direction of the vector is
`\mathbf{\hat i}`