Question

A mass m = 0.7 kg is released from rest at the origin 0. The mass falls under the influence of gravity. When the mass reaches point A, it is a distance x below the origin 0; when the mass reaches point B it is a distance of 3 x below the origin 0. What is vB/vA?

Answer 1

`v_B/v_A=√(3)`

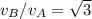
Step-by-step explanation:

Consider the two kinematic equations for velocity and position of an object falling due to the action of gravity:

`v=-g\,t\\ \\position=-(1)/(2) g\,t^2`

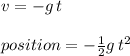
Therefore, if we consider
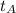`t_A` the time for the object to reach point A, and
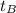`t_B` the time for it to reach point B, then:

`v_A=-g\,t_A\\v_B=-g\,t_B\\(v_B)/(v_A)= (-g\,t_B)/(-g\,t_A) =(t_B)/(t_A)`

Let's work in a similar way with the two different positions at those different times, and for which we have some information;

`x_A=-x=-(1)/(2)\, g\,t_A^2\\x_B=-3\,x=-(1)/(2)\, g\,t_B^2\\ \\(x_B)/(x_A) =(t_B^2)/(t_A^2) \\(t_B^2)/(t_A^2)=(-3\,x)/(-x) \\(t_B^2)/(t_A^2)=3\\((t_B)/(t_A))^2=3`

Notice that this quotient is exactly the square of the quotient of velocities we are looking for, therefore:

`((t_B)/(t_A))^2=3\\((v_B)/(v_A))^2=3\\ (v_B)/(v_A)=√(3)`