Question

An operator wants to determine the standard deviation for a machine relative to its ability to produce windshield wipers conforming within their specifications. To do this, she wants to create a p-chart. Over a month's time, she tests 100 units every day and records the number of manufacturing defects. The average proportion of non-conforming windshield wipers is found to be 0.042. What is the standard deviation of this sample

Answer 1

the standard deviation of the sample is less than 0.1

Explanation:

Given that :

The sample size n = 100 units

The average proportion of non-conforming windshield wipers is found to be 0.042 which is the defective rate P-bar

The standard deviation of the machine(
`S_p`) can be calculated by using the formula:

`S_p =( √( \overline P * (1 - \overline P)) )/(n)`

`S_p =( √(0.042 * (1 -0.042)) )/(100)`

`S_p =( √(0.042 * (0.958)) )/(100)`

`S_p =( √(0.040236) )/(100)`

`S_p =( 0.2005891323 )/(100)`

`S_p =0.002`

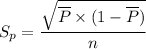
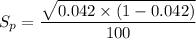
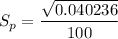
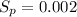
Thus , the standard deviation of the sample is less than 0.1