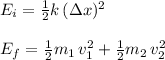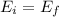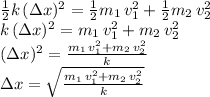Question

Two mass m1 and m2 lie on a frictionless surface. Between the two masses is a compressed spring, with spring constant k. The system is held in place. At time t=0 the blocks are released. The blocks move off in opposite directions with velocities v1 and v2. how much was the spring compressed?

Answer 1

The spring was compressed the following amount:

`\Delta x=\sqrt{ (m_1\,v_1^2+ m_2\,v_2^2)/(k) }`

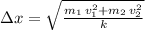
Step-by-step explanation:

Use conservation of energy between initial and final state, considering that the surface id frictionless, and there is no loss in thermal energy due to friction. the total initial energy is the potential energy of the compressed spring (by an amount
`\Delta x`), and the total final energy is the addition of the kinetic energies of both masses:

`E_i=(1)/(2) k\,(\Delta x)^2\\\\E_f=(1)/(2) m_1\,v_1^2+(1)/(2) m_2\,v_2^2`

`E_i=E_f\\`

`(1)/(2) k\,(\Delta x)^2=(1)/(2) m_1\,v_1^2+(1)/(2) m_2\,v_2^2\\k\,(\Delta x)^2=m_1\,v_1^2+ m_2\,v_2^2\\(\Delta x)^2=(m_1\,v_1^2+ m_2\,v_2^2)/(k) \\\Delta x=\sqrt{ (m_1\,v_1^2+ m_2\,v_2^2)/(k) }`