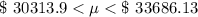Answer:
The 90% confidence interval is
Explanation:
From the question we are told that
The sample size is n = 64
The sample mean is
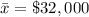
The standard deviation is
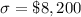
Given that the confidence interval is 90% then the level of significance is mathematically evaluated as
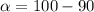
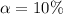
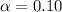
Next we obtain the critical value of
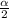 from the normal distribution table , the value is
from the normal distribution table , the value is
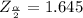
Generally the margin of error is mathematically represented as
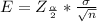
=>
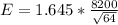
=>
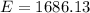
The 90% confidence interval is mathematically represented as
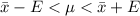
=>
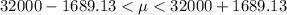
=>