Question

A diffraction grating 19.2 mm wide has 6010 rulings. Light of wavelength 337 nm is incident perpendicularly on the grating. What are the (a) largest, (b) second largest, and (c) third largest values of θ at which maxima appear on a distant viewing screen?

Answer 1

(a). The largest value of θ is 71.9°.

(b). The second largest value of θ is 57.7°.

(c). The third largest value of θ is 47.7° .

Step-by-step explanation:

Given that,

Width of diffraction grating
`w= 19.2\ mm`

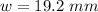
Number of rulings
`N=6010`

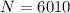
Wavelength = 337 nm

We need to calculate the distance between adjacent rulings

Using formula of distance

`d=(w)/(N)`

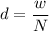
Put the value into the formula

`d=(19.2*10^(-3))/(6010)`

`d=3.19*10^(-6)\ m`

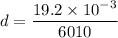
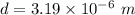
We need to calculate the value of m

Using formula of constructive interference

`d \sin\theta=m\lambda`

`\sin\theta=(m\lambda)/(d)`

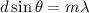
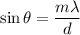
Here, m = 0,1,2,3,4......

`\lambda`=wavelength

For largest value of θ

`(m\lambda)/(d)>1`

`m>(d)/(\lambda)`

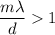
Put the value into the formula

`m>(3.19*10^(-6))/(337*10^(-9))`

`m>9.46`

`m = 9`

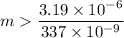
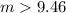
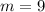
(a). We need to calculate the largest value of θ

Using formula of constructive interference

`\theta=\sin^(-1)((m\lambda)/(d))`

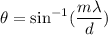
Now, put the value of m in to the formula

`\theta=\sin^(-1)((9*337*10^(-9))/(3.19*10^(-6)))`

`\theta=71.9^(\circ)`

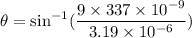
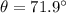
(b). We need to calculate the second largest value of θ

Using formula of constructive interference

`\theta=\sin^(-1)((m\lambda)/(d))`

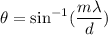
Now, put the value of m in to the formula

`\theta=\sin^(-1)((8*337*10^(-9))/(3.19*10^(-6)))`

`\theta=57.7^(\circ)`

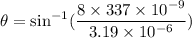
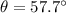
(c). We need to calculate the third largest value of θ

Using formula of constructive interference

`\theta=\sin^(-1)((m\lambda)/(d))`

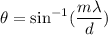
Now, put the value of m in to the formula

`\theta=\sin^(-1)((7*337*10^(-9))/(3.19*10^(-6)))`

`\theta=47.7^(\circ)`

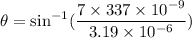
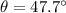
Hence, (a). The largest value of θ is 71.9°.

(b). The second largest value of θ is 57.7°.

(c). The third largest value of θ is 47.7° .