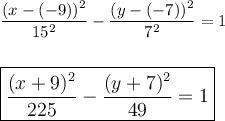Question

write the equation of a horizontal ellipse with a major axis of 30, a minor axis of 14, and a center at (-9,-7).​

Answer 1

Answer:
`((x+9)^2)/(225)-((y+7)^2)/(49)=1`

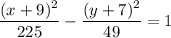
Explanation:

The equation for a horizontal ellipse is:
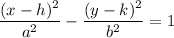`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1` where

• (h, k) is the center
• a is x-radius
• b is the y-radius

Given: major axis (diameter on x) is 30 --> x-radius (a) = 15 --> a² = 225

minor axis (diameter on y) is 14 --> y-radius (b) = 7 --> b² = 49

center (h, k) is (-9, -7)

Input those values into the equation for a horizontal ellipse and simplify:

`((x-(-9))^2)/(15^2)-((y-(-7))^2)/(7^2)=1\\\\\\\large\boxed{((x+9)^2)/(225)-((y+7)^2)/(49)=1}`