Question

The table shows the results of a survey in which 10th-grade students were asked how many siblings (brothers and/or sisters) they have. A 2-column table has 4 rows. The first column is labeled Number of siblings with entries 0, 1, 2, 3. The second column is labeled number of students with entries 4, 18, 10, 8. What is the experimental probability that a 10th-grade student chosen at random has at least one, but no more than two, siblings? Round to the nearest whole percent. 65% 70% 75% 80%

Answer 1

Explanation:

bB

Answer 2

70%

Explanation:

Given

Number of Siblings: || 0 || 1 || 2 || 3

Number of Students: || 4 || 18 || 10 || 8

Required

Determine the probability of a student having at least one but not more than 2 siblings

First, we have to determine the total number of 10th grade students

`Total = 4 + 18 + 10 + 8`

`Total = 40`

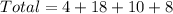
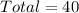
The probability of a student having at least one but not more than 2 siblings = P(1) + P(2)

Solving for P(1)

P(1) = number of students with 1 sibling / total number of students

From the given parameters, we have that:

Number of students with 1 sibling = 18

So:

`P(1) = (18)/(40)`

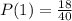
Solving for P(2)

P(2) = number of students with 2 siblings / total number of students

From the given parameters, we have that:

Number of students with 2 siblings = 10

So:

`P(2) = (10)/(40)`

`P(1) + P(2) = (18)/(40) + (10)/(40)`

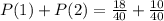
Take LCM

`P(1) + P(2) = (18 + 10)/(40)`

`P(1) + P(2) = (28)/(40)`

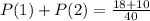
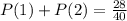
Divide numerator and denominator by 4

`P(1) + P(2) = (7)/(10)`

`P(1) + P(2) = 0.7`

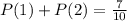
Convert to percentage

`P(1) + P(2) = 70\%`

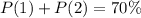
Hence, the required probability is 70%