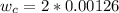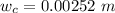Question

A single slit 1.5 mm wide is illuminated by 420- nm light. Part A What is the width of the central maximum (in cm ) in the diffraction pattern on a screen 4.5 m away

Answer 1

The width is
`w_c = 0.00252 \ m`

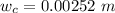
Step-by-step explanation:

From the question we are told that

The width of the single slit is
`a = 1.5 \ mm = 1.5 *10^(-3) \ m`

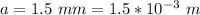
The wavelength is
`\lambda = 420 *10^(-9) \ m`

The distance of the screen is
`D = 4.5 \ m`

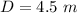
Generally the width of the central maximum is

`w_c = 2 * y`

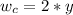
where y is the width of the first maxima which is mathematically represented as

`y = (\lambda * D)/(a)`

=>
`y = ( 420 *10^(-9) * 4.5)/( 1.5*10^(-3))`

=>
`y = 0.00126 \ m`

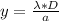
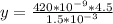
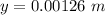
So

`w_c = 2 *0.00126`

`w_c = 0.00252 \ m`