Complete Question
Assume that random guesses are made for 7 multiple-choice questions on a test with 5 choices for each question, so that there are n=7 trials, each with probability of success (correct) given by p=0.20. Find the probability of no correct answers.
Answer:
The probability is
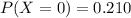
Explanation:
From the question we are told that
The number of trial is n = 7
The probability of success is p = 0.20
Generally the probability of failure is
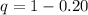
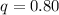
Given that this choices follow a binomial distribution as there is only two probabilities i.e success or failure
Then the probability is mathematically represented as
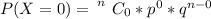
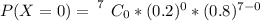
Here

=>
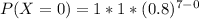
=>