Question

How much time will elapse if a radioisotope with a half-life of 88 seconds decays to one-sixteenth of its original mass?

Answer 1

352 seconds are needed for the radioisotope to decay to one-sixteenth of its original mass.

Step-by-step explanation:

The decay of radioisotopes are represented by the following ordinary differential equation:

`(dm)/(dt) = -(t)/(\tau)`

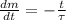
Where:

`t` - Time, measured in seconds.

`\tau` - Time constant, measured in seconds.

`m` - Mass of the radioisotope, measured in grams.

The solution of this expression is:

`m(t) = m_(o)\cdot e^{-(t)/(\tau) }`

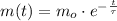
Where
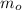`m_(o)` is the initial mass of the radioisotope, measured in kilograms.

The ratio of current mass to initial mass is:

`(m(t))/(m_(o)) = e^{-(t)/(\tau) }`

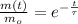
The time constant is now calculated in terms of half-life:

`\tau = (t_(1/2))/(\ln2)`

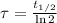
Where
`t_(1/2)` is the half-life of the radioisotope, measured in seconds.

Given that
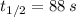`t_(1/2) = 88\,s`, the time constant of the radioisotope is:

`\tau = (88\,s)/(\ln 2)`

`\tau \approx 126.957\,s`

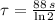
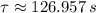
Now, if
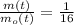`(m(t))/(m_(o)(t)) = (1)/(16)` and
`\tau \approx 126.957\,s`, the time is:

`t = -\tau \cdot \ln(m(t))/(m_(o))`

`t = -(126.957\,s)\cdot \ln (1)/(16)`

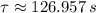`t \approx 352\,s`

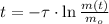
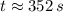
352 seconds are needed for the radioisotope to decay to one-sixteenth of its original mass.