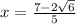The solution of the problem is
Given that:
The equation is
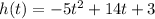 , where
, where
 is height .
is height .
The ball is
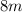 above the ground so
above the ground so
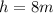 .
.
Now,
Substitute the value of height in given equation,
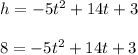
Subtract
 on both side to obtain the quadratic equation,
on both side to obtain the quadratic equation,
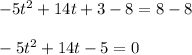
Multiply minus sign in both sides,
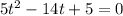
Solve the quadratic equation ,
Where,
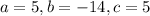
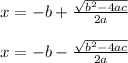
Substitute the known values in the formula,

Similarly,