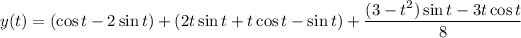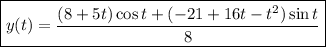Considering you have four initial conditions (the last of which should probably read
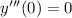 ), I'm assuming the ODE is
), I'm assuming the ODE is
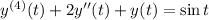
with
 ,
,
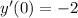 ,
,
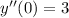 , and
, and
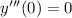 .
.
Take the Laplace transform of both sides, denoting the transform of
 by
by
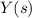 :
:
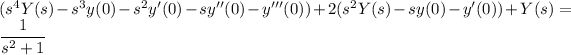
Solve for
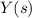 :
:


Notice that
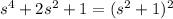
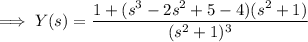
and simplify a bit to get
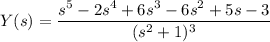
Decompose
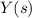 into partial fractions:
into partial fractions:
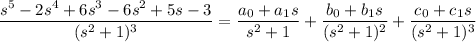
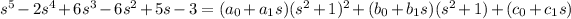
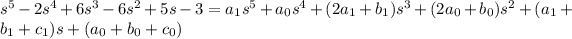
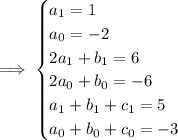

So we have
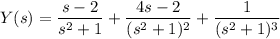
Split up the first term to get two easy inverse transforms:
![L^(-1)\left[\frac s{s^2+1}\right]=\cos t](https://img.qammunity.org/2021/formulas/mathematics/college/jbio5ei996uhmpu335tkjlvj3a1syr6ubq.png)
![L^(-1)\left[-\frac2{s^2+1}\right]=-2\sin t](https://img.qammunity.org/2021/formulas/mathematics/college/trrm4kn8lvidwv5do8qt7uej8q5mfwn1sf.png)
Also split up the second term, but use the convolution theorem, which says
![L\left[(\alpha \ast \beta)(t)\right]=A(s)\cdot B(s)](https://img.qammunity.org/2021/formulas/mathematics/college/l9d6uvwf55yx2m6gaycef1c2y4n48sey0n.png)
where
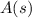 and
and
 are the Laplace transforms of
are the Laplace transforms of
 and
and
 , respectively, and the convolution is defined by
, respectively, and the convolution is defined by
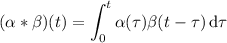
Take
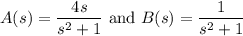
so that

and their convolution is
![L^(-1)\left[(4s)/((s^2+1)^2)\right]=(\alpha \ast \beta)(t)=2t\sin t](https://img.qammunity.org/2021/formulas/mathematics/college/3yaaqvp67zb6mexcfk2fas16ze0lvk6h17.png)
Next, take
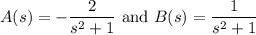
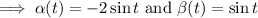
![\implies L^(-1)\left[-\frac2{(s^2+1)^2}\right]=t\cos t-\sin t](https://img.qammunity.org/2021/formulas/mathematics/college/eu1vjvr9iz7owngaaxl8nu1btt5iwmqy8i.png)
You can treat the third term similarly, but with an extra step. First compute
![L^(-1)\left[\frac1{(s^2+1)^2}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/e15z1wd3xhcfw2w6cvtpq9bk5gzl8dmufn.png)
by taking

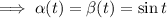
Then
![L^(-1)\left[\frac1{(s^2+1)^2}\right]=\frac{\sin t-t\cos t}2](https://img.qammunity.org/2021/formulas/mathematics/college/vlfahaxbi2f7vrf0i3u8zppd33m6xubrtg.png)
Next, take
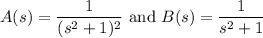

![\implies L^(-1)\left[\frac1{(s^2+1)^3}\right]=\frac{(3-t^2)\sin t-3t\cos t}8](https://img.qammunity.org/2021/formulas/mathematics/college/e9kxx43lmtls321h4embtmanz29s99irw0.png)
Thus we end up with the solution,