Question

Sum and Product of zeroes of the quadratic polynomial 16s² - 16s + 4 respectively is:Sum and Product of zeroes of the quadratic polynomial 16s² - 16s + 4 respectively is:​

Answer 1

The sum and product of zeroes are 1 and 1/4, respectively.

Explanation:

To determine the zeroes of the quadratic polynomial, let equalize the polynomial to zero and solve in consequence:

`16\cdot s^(2)-16\cdot s + 4 = 0`

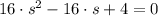
By the General Quadratic Formula:

`s_(1,2) = \frac{16\pm \sqrt{(-16)^(2)-4\cdot (16)\cdot (4)}}{2\cdot (16)}`

`s_(1,2) = (1)/(2)`

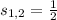
Which means that zeroes are
`s_(1)=s_(2)=(1)/(2)`.

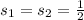The sum and product of zeroes are, respectively:

`s_(1)+s_(2) =(1)/(2)+(1)/(2)`

`s_(1)+s_(2) = 1`

`s_(1)\cdot s_(2) = \left((1)/(2) \right)^(2)`

`s_(1)\cdot s_(2) = (1)/(4)`

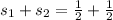
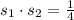
The sum and product of zeroes are 1 and 1/4, respectively.