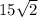Question

What is the square root of 450​

Answer 1

`15√(2)` or 21.2132

Explanation:

`√(450)`

`\sqrt{15^(2) }` (root of a product is equal to the product of the roots of each factor)

`\sqrt{15^(2) } √(2)` (simplify)

`15√(2)` or ≈ 21.2132

Answer 2

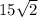`15√(2)` or 21.213

Explanation:

For radical form: think of multiples of 450. Think of a pair that contains one perfect square, particularly the higher, the better . These 2 numbers are 25 and 18. 25 is the perfect square number since the two numbers that multiply to be 25 is 5 and 5.

Now take the perfect square of 25 and put it outside of the radical. The 18 remains inside:
`5√(18)`

Now, since 18 is a high number that needs to get reduced, do the same for 18 as we did for 450--find two numbers, one of which is a perfect square. These two numbers are 9 and 2.

Now take the perfect square of 9. This is 3. Take it out of the radical so that only the two remains inside. The 3 will now multiply with the 5:
`5*3√(2)`

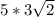
Multiply 5 and 3 to get 15. The 15 stays outside the radical. Your answer is:

`15√(2)`