Answer:
symbolically, the answer would be t= ln(2)/(.08)
Explanation:
start by writing out your variables:
rate= .08
*dont forget the investment doubles too, thats where 2P is in the bottom equation
equation should look like:
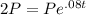
then you solve, so divide P on the right and left:
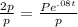
now it looks like:

you can take the natural log (ln) of 2 to get the exponent by itself .08t
ln(2)=.08t
then divide .08 to get t by itself

so symbolically, your equation should be:
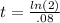
to get t as your answer you can plug this equation into your calculator to get:
t=8.66 years so approximently 8 years