Question

A fan rotating with an initial angular velocity of 1500 rev/min is switched off. In 2.5 seconds, the angular velocity decreases to 400 rev/min. Assuming the angular acceleration is constant, answer the following questions.

How many revolutions does the blade undergo during this time?
A) 10
B) 20
C) 100
D) 125
E) 1200

Answer 1

The blade undergoes 40 revolutions, so neither of the given options is correct!

Step-by-step explanation:

The revolutions can be found using the following equation:

`\theta_(f) = \theta_(i) + \omega_(i)*t + (1)/(2)\alpha*t^(2)`

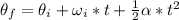
Where:

α is the angular acceleration

t is the time = 2.5 s

`\omega_(i)` is the initial angular velocity = 1500 rev/min

First, we need to find the angular acceleration:

`\alpha = (\omega_(f) - \omega_(i))/(t) = (400 rev/min*2\pi rad*1 min/60 s - 1500 rev/min *2\pi rad*1 min/60 s)/(2.5 s) = -46.08 rad/s^(2)`

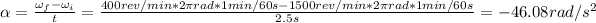
Now, the revolutions that the blade undergo are:

`\theta_(f) - \theta_(i) = \omega_(i)*t + (1)/(2)\alpha*t^(2)`

`\Delta \theta = 1500 rev/min *2\pi rad*1 min/60 s*2.5 s - (1)/(2)*(46.08 rad/s^(2))*(2.5)^(2) = 248.7 rad = 39.9 rev`

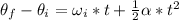
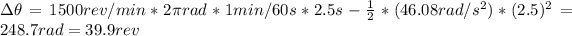
Therefore, the blade undergoes 40 revolutions, so neither of the given options is correct!

I hope it helps you!