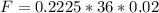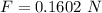Complete Question
A 590-turn solenoid is 12 cm long. The current in it is 36 A . A 2 cm straight wire cuts through the center of the solenoid, along a 4.5-cm diameter. This wire carries a 27-A current downward (and is connected by other wires that don't concern us).
What is the magnitude of the force on this wire assuming the solenoid's field points due east?
Answer:
The force is
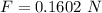
Step-by-step explanation:
From the question we are told that
The number of turns is
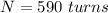
The length of the solenoid is
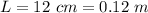
The current is
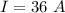
The diameter is
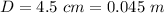
The current carried by the wire is
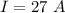
The length of the wire is
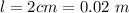
Generally the magnitude of the force on this wire assuming the solenoid's field points due east is mathematically represented as

Here B is the magnetic field which is mathematically represented as
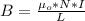
Here
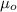 is permeability of free space with value
is permeability of free space with value
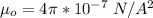
substituting values
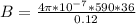
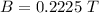
So