Question

A sample of radioactive silver contains two isotopes, 108Ag (denoted A) and 110Ag (denoted B). The second of these (B) has a half life of 24 seconds, whereas the first (A) has a half life of 2.3 minutes. If a sample contains equal numbers of each of these isotopes at the beginning of an experiment that runs for an hour, which of the following statements is correct?

A. At the end of the hour, isotope B has a greater decay constant λ than isotope A
B. At the end of the hour, isotope A has the same decay constant λ as isotope B
C. At the end of the hour, isotope A has a greater decay constant λ than isotope B

Answer 1

A : At the end of the hour, isotope B has a greater decay constant λ than isotope A

Step-by-step explanation:

Firstly, we need to understand that radioactive decay follows a first order rate law.

What this means is that we can calculate the radioactive decay constant using the following formula from the half-life

Mathematically;

`t_(1/2)` = 0.693/λ

where λ represents the radioactive decay constant.

Rearranging the equation, we can have

λ = 0.693/
`t_(1/2)`

Now, to have a fair level playing ground, it is best that the half-life of both isotopes are in the same unit of time(seconds)

For A, the half-life = 2.3 minutes which is same as 2.3 × 60 = 138 seconds

For B, the half-life is 24 seconds

Thus, at the end of the hour, the decay constant for isotope A will be;

λ = 0.693/138 = 0.0050
`s^(-1)`

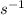
For isotope B, the decay constant will be;

λ = 0.693/24 = 0.028875
`s^(-1)`

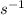
We can see that the decay constant of isotope B is higher than that of A at the end of the experiment